Alice and Bob use the Diffie–Hellman key exchange technique.

Question 10.1:

Alice and Bob use the Diffie–Hellman key exchange technique with a common prime
q = 1 5 7 and a primitive root a = 5.
a. If Alice has a private key XA = 15, find her public key YA.
b. If Bob has a private key XB = 27, find his public key YB.
c. What is the shared secret key between Alice and Bob?

Solution:

We are given that q= 157 and a primitive rot a=5.

1. If Alice has a private key XA=15, find her public key YA.

So, public key for Alice will be given as

YA= (a) ^xa Mod (q)

     = (5)¹⁵ mod (157)

     = 79

1. If Bob has a private key XB = 27, find his public key YB.

So, public key for Bob will be given as

YB= (a) ^xb mod (q)

     = (5)²⁷ mod (157)

     = 65

1. What is the shared secret key between Alice and Bob.

Shared key (for Alice) = (YB) ^xa mod (157)

= (65)¹⁵ mod (157)

= 78

Shared key (for bob) = (YA) ^xb mod (q)

= (79)²⁷ mod (157)

= 78

Thus, shared secret key between Alice and Bob is 78.

Question 10.2:

Alice and Bob use the Diffie-Hellman key exchange technique with a common prime q = 2 3 and a primitive root a = 5 . a. If Bob has a public key YB = 1 0 , what is Bob’s private key YB? b. If Alice has a public key YA = 8 , what is the shared key K with Bob? c. Show that 5 is a primitive root of 23.

Solution:

1. If Bob has a public key YB = 1 0 , what is Bob’s private key YB.

Given common prime q = 23

Primitive root a = 5

Bob has a public key YB= 10

Bob’s private key BX = ?

YB = a^XB (mod 23)

YB = 5XB (mod 23) (∴ q=23)

10 = 5^XB (mod 23)

 ∴5¹ mod 23 = 5

               5² mod 23 = 25 mod 23 = 2

               5³ mod 23 = 125 mod 23 = 10

            ∴ 5³(mod 23) = 5^XB (mod23)

            = XB = 3

∴ Bob’s private key XB = 3

1. If Alice has a public key YA = 8 , what is the shared key K with Bob.

Alice has a public key YA= 8

The shared key K with Bob = ?

K= YA^XB(mod q)

K = 8³(mod23)

K= 512(mod23)

K= 6(mod 23)

∴ K=6 is the shared key with Bob.

23. Show that 5 is a primitive root of 23

In order to check whether 5 is a primitive root of 23 we need to construct a table for it as shown below:

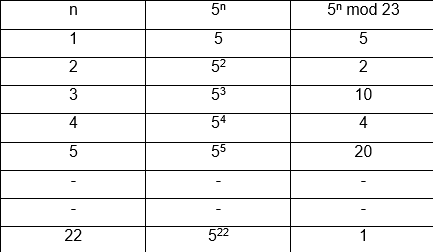
            ∴ 5²² = 5⁴ x 5⁴ x 5⁴ x 5⁴ x 5⁴ x 5² 

        = (4x 4 x 4 x 4 x 4  x 2) (mod 23)

        = 16 x 16 x 8 (256 x 8) (mod23)

        = 24 (mod 23)

        = 1

Thus 5 is a primitive root of 23.

Question 10.3:

In the Diffie-Hellman protocol, each participant selects a secret number x and sends the other participant αx mod q for some public number α. What would happen the participant if the participants sent each other Xα instead? Give at least one method Alice and Bob could use to agree on a key.   Can Eve break your system without finding the secret numbers? Can Eve find the secret numbers?

Solution:

If the participant sends xα instead of sending αx mod q then the system will be insecure and can be broken easily. As α is the public number, the intruder (Eve) also knows it and he can get the key value by just dividing the message sent from the participant by α. So security of system fails.

One method that Alice and Bob can agree on the key is the conventional Diffie-Hellman algorithm. In this, two numbers p and g are made public where p is a large prime number and g is the primitive root modulo p and there are two private numbers on each side (let sender side has a and the receiver side has b). Key is generated in two steps

• First the sender sends (R₁= g^a mod p) to the receiver and receiver sends (R₂= g^b  mod p) to the sender.
• Then sender generates the key as: key=(R ₂)^a mod p =g^ab  mod p and the receiver generates the key as: key =(R₁)^b mod p= g^ab mod p

This way sender and receiver get the same key without transferring the key directly

Without knowing the key Eve cannot break the system but it can hinder the system by modifying the message sent by the sender.

By applying the above-mentioned technique of key generation for the system its become almost impossible to Eve to find the secret key.

Question 10.4:

This problem illustrates the point that the Diffie-Hellman protocol is not secure without the step where you take the modulus; i.e. the “Indiscrete Log Problem” is not a hard problem! You are Eve and have captured Alice and Bob and imprisoned them. You overhear the following dialog.

Bob: Oh, let’s not bother with the prime in the Diffie-Hellman protocol, it will make things easier.

Alice: Okay, but we still need a base a to raise things to. How about a = 3? Bob: All right, then my result is 27.
Alice: And mine is 243.

What is Bob’s private key XB and Alice’s private key XA? What is their secret combined key?

Solution:

• Alice and Bob agree to not to use a modulus.
•  Bob chooses a secret integer a = 3.
•  Bob : B = g^a = 27 => g = 3
•  Alice : A = g^b = 243 = > b = 5
• Alice computes s = B^b
  s = 27⁵ = 3¹⁵
•  Bob computes s = A^a
  s = 243³ = 3¹⁵
  
  Xb = 3
  Xa = 5
  combined = 3¹⁵

Question 10.5:

Describes a man-in-the-middle attack on the Diffie-Hellman key ex-change protocol in which the adversary generates two public–private key pairs for the attack. Could the same attack be accomplished with one pair? Explain

Solution:

• Darth prepares for the attack by generating a random private key X_D and then computing the corresponding public key Y_D.
• Alice transmits Y_A to Bob.
• Darth intercepts Y_A and transmits Y_D to Bob. Darth also calculates K₂ = (Y_A )X_D mod q
•  Bob receives Y_D and calculates K₁= (Y_D )X_B mod q .
• Bob transmits X_A to Alice.
• Darth intercepts X_A and transmits Y_D to Alice. Darth calculates K₁= (YD )X_D mod q.
• Alice receives Y_D and calculates K₂ = (Y_D ) XA mod q .

At this point, Bob and Alice think that they share a secret key, but instead Darth share Secret key K1 to Alice and K2 to Bob. All future communication between Bob and Alice is compromised in the following way:

1. Alice sends an encrypted message M:E(K2,M).

2. Darth intercepts the encrypted message and decrypts it, to recover M.

3 .Darth sends Bob E(K1,M) or E(K1,M’), where M’ is any message. In the first case, Darth simply wants to eavesdrop on the communication without altering it. In the second case, Darth wants to modify the message going to Bob.

Question 10.9:

 Is (5, 12) a point on the elliptic curve y2 = x 3 + 4 x – 1 over real numbers?

Solution:

Equation of curve: y² = x³ + 4x-1

Any point satisfying this equation (x³+4x-1-y² =0)

= F(x,y) must lie on this curve

We have to check whether this is true for (5,12)

F (5,12) = 5³ + 4.5-1-12² = 0

Thus, (5,12) lies on the curve.

Question 10.15:

This problem performs elliptic curve encryption/decryption using the scheme out- lined in Section 10.4. The cryptosystem parameters are E11(1, 7) and G = (3, 2). B’s private key is nB = 7.
a. Find B’s public key PB.
b. A wishes to encrypt the message Pm = (10, 7) and chooses the random value
k = 5. Determine the cipher text Cm.
c. Show the calculation by which B recovers Pm from Cm.

Solution:

1. Find B’s public key PB.

To find B’s public key, the formula is p_B = n_B x G

= 7 x (2, 7)

= (7, 2)

Therefore B’s public key p_B = (7, 2)

• A wishes to encrypt the message Pm = (10, 7) and chooses the random value
  k = 5. Determine the cipher text Cm.

To find cipher text, the formula is C_m = {kG, p_m + kP_B }

= {3(2, 7), (10, 9) + 3(7, 2)}

= {(8, 3), (10, 9) + (3, 5)}

= {(8, 3), (10, 2)}

Therefore cipher text C_m = {(8, 3), (10, 2)}

• Show the calculation by which B recovers Pm from Cm.

To find B Recovers, formula is P_m = {kP_b – n_b (kG, P_m)}

= (10, 2) – 7(8,3)

=(10, 2) – (3,5)

= (10, 2) + (3, 6)

= (10, 9)

Addition and multiplication between two points are proceeding from the table.

Question 10.16:

The following is a first attempt at an elliptic curve signature scheme. We have a global elliptic curve, prime p, and “generator” G. Alice picks a private signing key XA and forms the public verifying key YA = XAG. To sign a message M:
■ Alice picks a value k.
■ Alice sends Bob M, k, and the signature S = M – kXAG.
■ Bob verifies that M = S + kYA.
a. Show that this scheme works. That is, show that the verification process produces
an equality if the signature is valid.
b. Show that the scheme is unacceptable by describing a simple technique for forging
a user’s signature on an arbitrary message.

Solution:

1. Show that this scheme works. That is, show that the verification process produces
   an equality if the signature is valid.
   To verify the process, the required elements are
2. Verified message by Bob that is M = S + KY_A
3. SignatureS = M – k X_AG
4. And public key Y_A = X_AG

Therefore, M = S + KY_A

M = M + k X_AG + k (X_AG), Where S, Y_A are taken from 2, 3

• Show that the scheme is unacceptable by describing a simple technique for forging
  a user’s signature on an arbitrary message.

To forging a message,

1. Intruder taking public key of Alice Y_A
2. And send message M, any value of k, and signature S = M – k Y_A